第二章 色彩空间的历史书
- Color
- 十分钟系列
第二章 色彩空间的历史书
2.1 色彩空间的历史
俗话说的好,想要了解一个事物,都要了解它的历史。很多当前的现象都是尤其长久的历史原因的。比方说为什么中国的用电是220V?为什么感冒了要刮痧?为什么小时候爸妈都是说你是捡来的……
如果想要了解为什么色彩空间会变成现在这个样子,就非常有必要聊聊有关历史,当读完了这本历史书之后,你可能就会明白一些为什么会有那么多的色彩空间、为什么色彩空间能够相互转换(可能吧……)
2.2 历史的车轮,谁也无法阻挡
科学的进步都不是一蹴而就的,往往中间会走不少的弯路,有的时候甚至会发现之前的结论完全是错误的。色彩科学的历程也是如此。但是一旦某个结论被公认是正确,那么之后的更多发现就会在此基础上帮助色彩科学的发展。
2.3 混沌的猜测年代【1800】
我们先飞到18XX 的年代,那个年代色彩科学的各种基础理论都是一片混沌。
为什么?因为人们还没有搞懂一件最重要的事情:
人类感觉色彩的机制是什么?
于是乎,人类就开始了大胆的猜测。那个时候差不多有三种猜测:
猜测1:人们有100多种的感受色彩的细胞
这种猜测的理由是,因为人们能够看到棱镜分光后的各种色彩。所以每种颜色对应一种感受色彩的细胞,于是就有100多种感色细胞。
这种猜测现在看来真的是非常的简单粗暴,而且被时间证明是扯淡的。
猜测2:人们有3种感色细胞,分别感受红、绿、蓝
也就是俗称的三色理论。
这种猜测有很多的事实根据的,因为当时人们发现色彩是可以通过三种基色进行混合的。而且神经科学也发现了视网膜上面的三种椎状细胞(LMS)。因此这套理论在当时迅速占据了主流。
猜测3:人们有3种感色细胞,但是感受的是3对色彩
和三色理论相同,这个理论也认为人类有三种感色细胞。但是三种细胞不是对应感受红、绿、蓝,而是感受三对色彩:
- 黑——白
- 红——绿
- 黄——蓝
这个理论也有直观的现象支持:比方说我们可以感觉到红里发黄 、绿里发黄、蓝里发红……但是从来没法感受到红里发绿、黄里发蓝。这就是补色的关系由来。
最后你猜怎么着,哪一个才是正确的?
猜测2 + 猜测3, 合在一起就形成了当下的色彩视觉模型
2.4 Munsell 色彩系统【1905】
在某些人们忙着搞清楚色彩感知原理的时候,另外一部分人也没闲着。
Albert Henry Munsell,美国艺术家,利用自己的艺术特长提出了Munsell 色彩系统。这个色彩系统后来被Committee of the Optical Society of America (OSA) 在1930 年优化。

Munsell 通过很多色卡来描述色彩。
- 旋转的角度是
Munsell 色相 - 垂直的方向是
Munsell 的亮度值 - 从圆心向外的方向是
Munsell 饱和度
可以看得出来,Munsell 的确是艺术家,因为人们凭借主观感受来区分色彩的依据正好就是HSL。
这个系统里面没有过多的物理科学在其中,更多的是一种归纳和规范。但是Munsell 色彩系统也为量化描述色彩提供了一种方式。这是非常值得称赞的。
在这之前,人们交流色彩的时候可能是:
“比苹果更红”
“鱼肚白”
“微微的清灰”
这些非常模糊的表述其实很难有统一的理解,当使用了Munsell 色彩系统后,一个颜色可以通过
H = 1.6YR
V = 6.3
C = 3.9
这种方式来表述,如果我们都有一个Munsell 色彩系统的标准色卡,那么就可以得到近似的颜色了。
2.5 CIE 1931 RGB Color Specification System 【1931】
虽然上面通过直观感受来量化描述的 Musell 色彩系统已经比文字描述好了很多,但是科学家们还是不满足,因为这不是最精确的“物理科学”级别的描述。我们需要一种完全客观的方式来描述色彩。
于是Commission Internationale de l’Eclairage (CIE)在1931年建立了一套色彩系统,希望能够完全客观的量化色彩。
此RGB 非彼RGB
很多人一看到RGB 就觉得这就是现在常说的那个RGB 色彩模型,一个立方体的盒子。
不不不!要说到你理解的那个RGB 还有好多年要走…… 这两个RGB 八杆子打不着。
观察者色彩匹配实验
不幸的是,在色彩科学中不存在“完全的客观”。因为最后总是需要人来看颜色,人就是主观的。
于是就需要想办法尽可能的弱化这部分主观可能导致的误差。CIE 的科学家想出了一个实验:
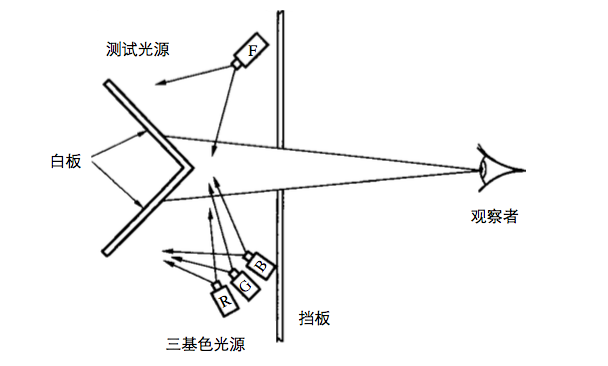

- 观察者通过一个挡板上面的洞看到后面的两个白板;
- 右边的白板被某个测试光源照亮,左边是被RGB 三个基色混合照亮。
- 要求观察者,通过调整RGB 三个光源的强度,使得左右两边的颜色看起来一样。
- 然后,记录下此时RGB 三基色分别的强度数值。如果用公式来表示:
【测试光源】 = r * [R] + g * [G] + b * [B]
[R]、[G]、[B] 表示三个基色,r、g、b 分别对应三种基色的强度。
这个公式表示的就是色彩的加色混合原理。
三基色的波长 [R]、[G]、[B] 是三基色,CIE 当然也为他们选择了特定的波长:
- [R] = 700.0 nm
- [G] = 546.1 nm
- [B] = 435.8 nm
色彩匹配方程
CIE 很有耐心的把从380 nm ~ 780 nm 波长中所有的光线都作为测试光,一个一个的重复上面的实验。
就得到了类似如下的数据:
- 380 nm = 0 * [R] + 0 * [G] + 0.01 * [B]
- 381 nm = 0 * [R] + 0 * [G] + 0.02 * [B]
- ……
- 780 nm = 0.01 * [R] + 0 * [G] + 0 * [B]
然后,我们把所有的数值都画在一张图表上面。就得到了三条曲线,这就是色彩匹配的信息。

如果你很细心的观察,你会发现有从435.8 nm ~ 546.1 nm 这段波长中,红色基色的强度竟然是负值?!
难道还能出现吸收光亮的光线么?!
当然是不可能的,造成这个的原因是在这个波段中,测试者不论怎么努力的调整三基色的强度都无法让混合后的颜色与测试光源的颜色相同;最后只要在测试光源的那一侧混入一定量的红色才使得左右两边看起来颜色相同。
这个通过公式来说就是:
【测试光源】+ r * [R] = g * [G] + b * [B]
(等式两遍同时减去 r * [R])
【测试光源】 = -r * [R] + g * [G] + b * [B]
这就是为什么出现了红色基色的强度出现了负值。
归一化
上面的色彩匹配方程其实已经完全足够了,但是科学家有个癖好,总是希望参数都是-1~1 之间的。这一步操作就叫做归一化。
归一化的计算也是异常的简单,原理就是算出每种基色强度在当前混色强度中所占的比例:
r' = r / (r+g+b)
g' = g / (r+g+b)
b' = b / (r+g+b)
经过这样的计算之后,r'、g'、b' 就都是在-1 ~ 1 之间了。而且很明显,我们发现 r' + g' + b' = 1。
这么说的话,我们只需要知道r'、g'、b' 三个参数中的任意两个,剩下的一个总是可以通过 1 - r' - g' 来得到。
也就是说,我们没有必要使用三个参数啦!只需要两个就够了!这也是归一化的另外一个优点。
图像化
这一步需要你稍微有点空间想象能力啦!
因为我们已经对数值进行归一化,因此只需要两个变量就足够表示所有的信息.
这里我们选择 r'、g' 这两个参数,那么b' = 1 - r' - g' 是可以随时计算出来的。
所以我们画个图表,横坐标是r',纵坐标是g' ,然后把所有的数值都画在这个图表上,就得到了:

如果你仔细看看,会发现有很多波长的色彩都落在了 -r' 的区域,还有一点点落在了 -g' 的区域。
不管你懂不懂,总之只要你知道这是人类的色彩科学历史上第一次可以客观的来描述一个颜色!我们可以把任何一个可见光的颜色用这个图表中的一个点的坐标来表示。
当然这个RGB 色彩标准还有很多使用上的不便,之后科学家会通过各种方法来对他进行优化,来达到各式各样的目的:
简化计算
方便感知
奇奇怪怪的需求
不过,对于后来所有的色彩空间、色彩标准,这个CIE 1931 RGB color specification system 绝对是色彩历史上的第一步!
一个小插曲:
CIE 1931 年观察者实验中的实验数据,其实只有 Guild 测试的7个人再上 Wright 测试的10个人……总共只有17个人。
现在动不动就大数据的年代,当时只有17个人…… 真是太简陋了。
2º 观察者
可能有很多人见过“2º 观察者” 这个名字,这是怎么回事?
其实,这个“2º 观察者” 就是从CIE 1931 RGB 来的。因为在当时的色彩匹配实验中,用户可以看到的视角只有2º。
2º 的视角是什么感觉? 假设有一张纸距离你 25 cm,在上面画一个半径 4.36mm 的圆圈,恩,这时候你的视角就是2º……

为什么看这么小的角度?CIE 当时有如下的考虑:
- 视网膜上有个中心凹,这个地方有着最高的视觉分辨力,而这个中心凹对应的视角差不多是2º
- 视网膜居中的区域有斑色素,如果超过4º 的视角,整个匹配结果就会有很大的变化
怎么样?听起来这两个理由是不是很有说服力?在一定程度上的确是非常好的考虑。
但是,还是那句话,色彩的感知还有很多生理上的特点。
例如,当你看到完全相同的两个颜色,只不过一个只是一个小圆点,另外一个是一整张A4 纸,你心理上的感觉会非常的不同。
再举个例子,装修刷墙的时候,你看到油漆小小的色卡,可能觉得某个颜色很适合,但是当这个颜色刷满一整面墙壁的时候,看起来的感觉可能会截然不同……(别问我怎么知道的!)
在这些条件的影响下,1959年,来自英国的 Stiles 和Burch,以及来自苏联的 Speranskaya 分别又做了色彩匹配实现,只不过这次,观看的视角变成了10º。
Stiles 和Burch 的实验有49个参与者,Speranskaya 邀请了18 个测试者(之后涨到27人)。这些结果成为1964 CIE Standard Colorimetric System。在这个色彩系统中,观察者自然就叫做“10º 观察者”。
2.6 XYZ Color Specification System 【1931年】
言归正传,CIE 1931 RGB 色彩系统看起来已经挺不错的了,但是他有一个很大的问题那就是存在负数!
虽然这个问题不会造成错误,但是对于实现计算来说就很麻烦。
试想一下,如果每次计算的时候都需要判断一下输入的是正数还是负数,就非常浪费时间了。
于是,人们就希望有一个新的色彩空间,可以满足以下的一些特性:
- 包含所有人眼可见光
- 所有 XYZ 数值都是正数,方便计算
- 三个色彩分量中的Y,可以直接表示光的亮度
- 如果光的波长 ≥ 650 nm,可以直接让 Z 分量 = 0,进一步简化计算
这里不讨论具体的细节,但是需要强调一下XYZ 色彩空间的意义。
首先,XYZ 色彩空间不是实验得到的,他是在CIE 1931 RGB 色彩系统的基础上,通过数学的手段得到的。
XYZ 色彩空间的目的主要就是为了简化计算,所以XYZ 可以说是一个非常好的“中转” 色彩空间。
比方说,如果你想从 A 空间 变成 B 空间,那么推荐的方式是实现 A 到 XYZ,再实现 XYZ 到B。
看起来浪费了一步,等色彩空间复杂起来之后,这种方式优势就大多了!

说了那么多,如果想要直接知道结论,这里就是:任何色彩空间的变换都可以理解为三维空间变换,所以只需要3x3 的矩阵就可以表示出来:

这里的RGB 是CIE 1931 RGB,可不是sRGB 里面的RGB 数值哦!
如果你有兴趣了解从CIE 1931 RGB 到 XYZ 的过程,可以看看线性代数哦……
归一化
当你有了三个变量,你想要用两个变量来表示……怎么办?
没错! 又是归一化!
和RGB 变成r、g 两个变量相同, 把XYZ 三个变量,变成x、y 两个变量,相当于求得了每个分量在总体中所占的比重:

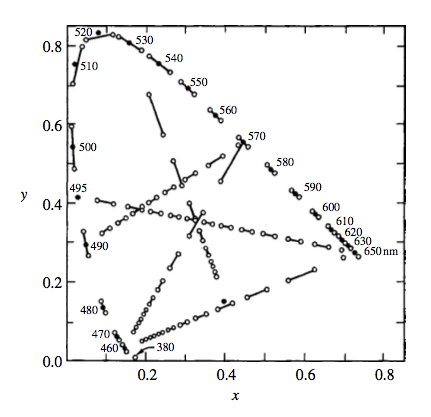
这时候,我们选择x、y 作为平面坐标系的两个轴,那么人眼所有可见的色彩范围是什么样子?

怎么样?是不是很熟悉?
没错,这就是传说中的人眼可见光范围的表示。
如果有细心的读者,没准可以发现,从这个图像上虽然可以分辨出所有的颜色,但是好像没有了亮度的区别?
比方说,有一个光线 c = (0.612, 0.256),我增强光线的强度或者降低光线的强度,人眼看到的颜色肯定不同,但是从 xy 来看,得到的坐标总是相同的……
没错,由于二维坐标 xy 只可能表示一个平面,那么亮度怎么办?
于是乎,在归一化 xy 的基础上,科学家们又把 XYZ 中的 Y 单独拿出来,与 xy 一起,组成了 Yxy 色彩空间。其中:
- Y 表示了亮度
- xy 表示了色度
这样就搞定了!
什么是 Yxy?对不起这里有点超纲啦……
总结
XYZ 色彩空间知道现在依然是极其重要的色彩标准之一。
当你需要计算色彩空间转换之类的时候,基本上一定会用到XYZ。
2.7 W*U*V* 和 L*a*b* 和 L*u*v* 【1964 - 1976】
别看花了眼睛,这里是三个色彩空间:
W*U*V*L*a*b*L*u*v*
怎么这次一口气来了三个色彩空间?因为它们三个有类似的特性。
有人可能会说,刚刚还在说XYZ 色彩空间如何如何好,怎么现在有需要的新的色彩空间了?
XYZ色彩空间的缺憾
没错,XYZ 色彩空间包含了所有可见光、计算简便、适合做“中转” 色彩空间,但是他有一个缺憾:色彩分布不是均匀的。
这要怎么理解?我们来举个例子:想象有一张地图,你家住在A 点,你公司在B 点。AB 之间的直线距离是d,完美情况下(你可以穿墙、走直线距离、没有红绿灯……)你需要T 分钟走到公司。有一天你搬家了,搬到了C 点,新的公司在D。凑巧的是CD 之间的距离也是d,那么完美情况下,你也只需要T 分钟走到公司。这很符合常识,没有问题。
我们回到上一节的 xy 色度坐标。我有一个颜色A,和另一个颜色B。AB 之间的距离是d,看起来的颜色差异是T。我们选择另外一组颜色C和颜色D,CD 之间的距离也是d,那么色彩看起来的差异也应该是T,对吧?很可惜,答案是NO。

比方说,我用相同长度的箭头表示在xy 色度坐标下的距离,可以明显看出,绿色区域内的箭头两端看起来差异比较小,而蓝色区域的差距就很大。
这就造成一个问题,我很难通过只计算两个颜色的之间的距离,就能够直观的感受到两个颜色之间的差异有多大。
uniform 类型的色彩空间
为了解决这个问题,就出现了一类叫做uniform colorspace 的色彩空间。【人欲无穷啊……】
“看起来差异差不多” 这件事情是一个主观的判断,当色彩科学中一遇到主观问题的时候,我们就需要“做实验”!
Wright 在1941年给出了一组数据,在相同的照明情况下,不同颜色可以分辨出的细小不同。
这些小短线表示的是可以发觉出颜色不同的距离。
线段长,表示颜色在坐标数值上需要变化很多,人眼才能发现不同。
线段短,表示只需要变化很小的坐标,人眼就会发觉颜色不同。
后来,Wright 和Pitt 一起对单波长的光线进行了这种测试,调整不同波长光线的强度,直到人眼“将将可以分辨”出区别(JND, just-noticeable difference)。
后来1942年,David Lewis MacAdam 又做了一个更详细的实验。和Wright 只在某个方向上测量将将可以分辨出色彩差异的坐标距离不同,MacAdam 测量了一个范围,这个范围内的颜色都是人眼发觉不出区别的。
于是乎,上面图像中的线段,就变成了下面这个图片中的一个个椭圆:

我们的最终目的就是希望有个新的色彩空间,是**“均匀分布”**的。
换句话说,就是通过某种变形,让上面图片中的椭圆,都变得差不多大。
这样就保证了坐标距离相同的情况下,色彩的差异性也是相同的。
于是CIE 在1960年使用了MacAdam 的转换方程,将xy 色度坐标,转换为uv 色度坐标:

通过这样的变换,xy 色度坐标内的那些椭圆就变成了下面的样子(虽然不对,但是可以试着这样理解一下,把上面xy 色度坐标上下挤压一下,左右拉伸一下,最后再非均匀的从下方往上方周围推推,好像橡皮泥一样):

怎么样,是不是现在看起来就均匀多了?
现在色度的均匀解决了,接下来就是亮度了。Yxy 中的 Y 所表示的亮度也存在非均匀的问题,因此还需要对亮度进行处理。
Wyszecki 在CIE 1960 uv 色度坐标的基础上提出了下面的W*U*V* 色彩空间:

这就是CIE 1964 W*U*V* 色彩空间。
这个色彩空间现在的人知道的应该不是很多了,因为在1976年,CIE 推荐使用两个新的色彩空间,这两个色彩空间就是 L*a*b* 和 L*u*v。相信这两个色彩空间知道的人就多很多了,不过注意,上面都是有*号的哦!要专业!
这里不会再进一步列举每个色彩空间的公式了(有兴趣可以去搜索维基百科,里面的解释很详细)。
对于读者来说更重要的是知道 L*a*b* 和 L*u*v* 这两个色彩空间,L* 都是对亮度进行了uniform 处理,同时色度坐标也是uniform 的。
回忆一下上面关于地图上家到公司之间的距离那个例子,现在在这种均匀的色彩空间内,两个颜色坐标之间的距离(欧氏距离),就可以代表人眼看到他们实际上相差的有多大了!假设AB 两个颜色之间的距离为0.2,另外两个颜色CD 之间的距离是0.47,你就可以非常有信心的说:“CD 看起来的差异比AB 要大!”
总结
这一节说的内容有点多…… 也有点枯燥……
但是一定要知道XYZ 色彩空间直到现在依然是极其重要的色彩标准之一,当你需要计算色彩空间转换之类的时候,基本上一定会用到 XYZ。
而L*a*b* 和 L*u*v* 这两个色彩空间 也是目前最常用的uniform 类型的色彩空间,在反应实际色彩感知的时候,这种均匀的色彩空间会帮你更多~
小编注:色彩空间的历史书就更新到这里了,Andy 没兴趣写下去了...... 下面就上干货了。

