计算反向 LUT
- Color
- 三十分钟系列
计算反向 LUT
经常会有需求,对于一个LUT 进行求逆。
如果是 Arri 这种文档详细的公司,那么可以得知具体的算法,那么肯定可以得到反向LUT。
但是很多情况下,我们只有LUT,在这种情况下,得到“精确”的反向LUT 会非常困难:
- 摄影机厂家自己提供的转换
LUT - 某些特定的调色
LUT
反向LUT 的求解困难
反向求解LUT 的困难主要存在以下几个方面:
LUT存在 “多对一” 的映射关系,反向求解无法还原精确的结果- 可能存在
LUT超界的情况。正向LUT导致超过1,而反向LUT只能还原一部分 - 正向
LUT的src是等间隔的lattice,但是映射后由于存在插值的情况,导致dst会落在lattice中间。所以反向LUT的src并不会直接对应正向LUT中的结果
第一个、第二个问题,这是无法解决的。
对于第三个问题,我们可能会有很多算法来解决。
我们使用2D 的grid 来说明这个问题:
正向 LUT 的 src

正向 LUT 的 dst
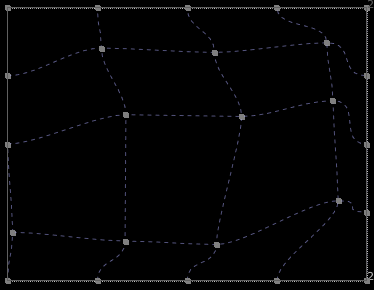
如何求解反向LUT src 对应的 dst?
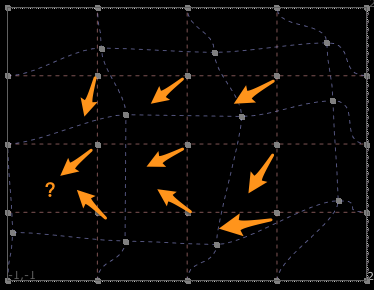
利用机器学习的思路来解决 lattice 对位
于是,有了一个思路。
我们可以通过不断的穷举 src 中的某个具体颜色c,通过正向LUT 变换后,得到的c'
直到c' 落在对应的lattice 网格上。
此时c' 就是反向的LUT 的src shaper,c 就是反向LUT 中的dst 数值
很明显,这里的穷举肯定会有一些技巧。对于一个“好” 的LUT 来说,至少会满足几个特性:
- 实际光照强度和
code value应该是单调递增的关系(不会出现越亮反而数值越小) - 只存在“压缩” 的情况,而不存在完全变成一个数值的情况(多对一)
这就正好利用了梯度下降的思路。
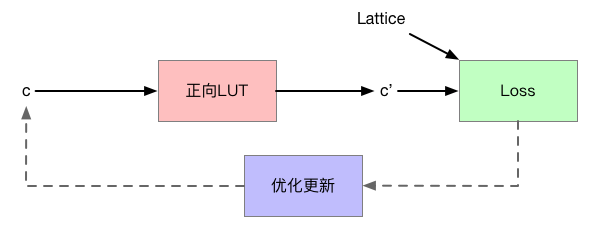
代码实现
详情
import colour
import numpy as np
import torch
import torch.autograd as autograd
import torch.nn as nn
import torch.optim as optim
from colour.algebra import table_interpolation_tetrahedral
class Tetrahedral(autograd.Function):
@staticmethod
def forward(ctx, input, lut):
ctx.lut = lut.table
ctx.input = input
result = table_interpolation_tetrahedral(
input.clone().detach(), lut.table)
return torch.from_numpy(result)
@staticmethod
def backward(ctx, grad_output):
input, lut = ctx.input, ctx.lut
delta = 1e-5
f_plus_delta = input.clone().detach()
f_plus_delta += delta
f_minus_delta = input.clone().detach()
gradient = (table_interpolation_tetrahedral(f_plus_delta, lut) -
table_interpolation_tetrahedral(f_minus_delta, lut)) / delta
return (torch.from_numpy(gradient) + torch.randn(gradient.shape)*0.03) * grad_output, None
class LUT:
def __init__(self, lut_path):
self.forward_lut = colour.read_LUT(lut_path)
self.backward_lut = None
self.backward_lut_step = None
def invert(self, step=33, error=1e-5, max_iter=10000, clamp=True):
mesh_x, mesh_y, mesh_z = torch.meshgrid(torch.linspace(0, 1, step),
torch.linspace(0, 1, step),
torch.linspace(0, 1, step))
lattice = []
for item in zip(mesh_x.reshape(-1),
mesh_y.reshape(-1),
mesh_z.reshape(-1)):
lattice.append([item[2].item(), item[1].item(), item[0].item()])
lattice = torch.tensor(lattice, dtype=torch.float64)
X = torch.ones(step**3, 3) * 0.5
X.requires_grad_()
interpolate = Tetrahedral.apply
criterion = nn.MSELoss()
optimizer = torch.optim.Adam([X], lr=1e-2)
epoch = 0
while epoch < max_iter:
optimizer.zero_grad()
Y = interpolate(X, self.forward_lut)
loss = criterion(Y, lattice)
loss.backward()
optimizer.step()
print(f'{epoch} loss = {loss}')
epoch += 1
self.backward_lut = X
if clamp:
self.backward_lut = torch.clamp(self.backward_lut, 0, 1)
self.backward_lut_step = step
return self.backward_lut
def save_invert_lut(self, cube_path):
if self.backward_lut is None:
raise Exception(
'place run .invert() method before .save_invert_lut()')
result_string = f'LUT_3D_SIZE {self.backward_lut_step}\n'
result_string += '\n'.join(
(f'{p[0]:.06f}\t{p[1]:.06f}\t{p[2]:.06f}' for p in self.backward_lut))
with open(cube_path, 'w') as f:
f.write(result_string)
if __name__ == '__main__':
lut = LUT('/Users/andyguo/Desktop/Slog3-S-Gamut3.Cine_To_s709.cube')
result = lut.invert(step=33, max_iter=100000)
print(result)
lut.save_invert_lut('/Users/andyguo/Desktop/invert_sony_600.cube')
算法效果
以sony slog3 sgamut3.cine to s709 的LUT 为例。
进行反向求解,在解算过程中所有误差的统计信息如下:
err_rate 0.5272003784400479
min: 0.0
max: 0.0156503826299
mean: 8.41535125187e-05
var: 7.76369308248e-08
median: 3.4147489589e-05
从空间的lattice 也可以看出,比较好的抵消了正向LUT 的变化。使得结果在有效范围内回归到标准lattice 平直的状态。
| 标准lattice | 正向LUT | 正向+ 反向抵消 | |
|---|---|---|---|
| top |  |  | 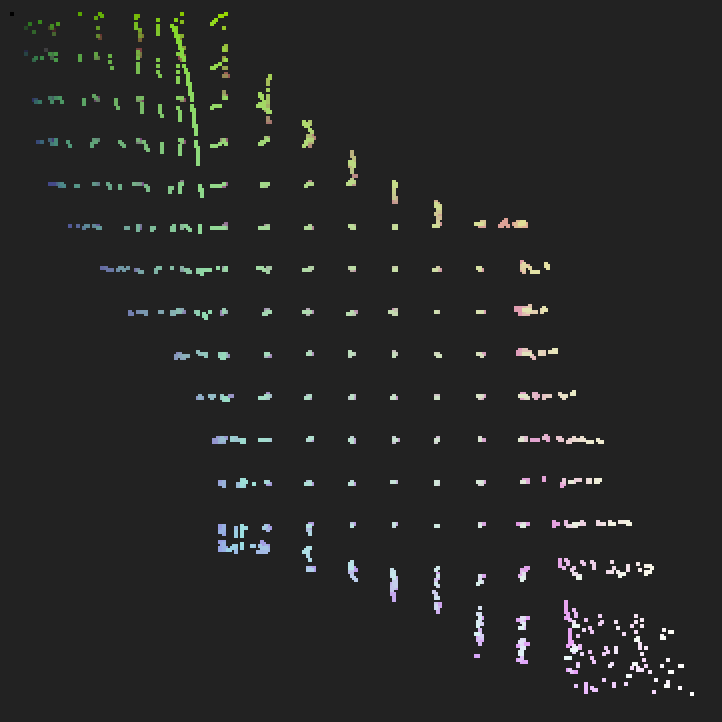 |
| front |  | 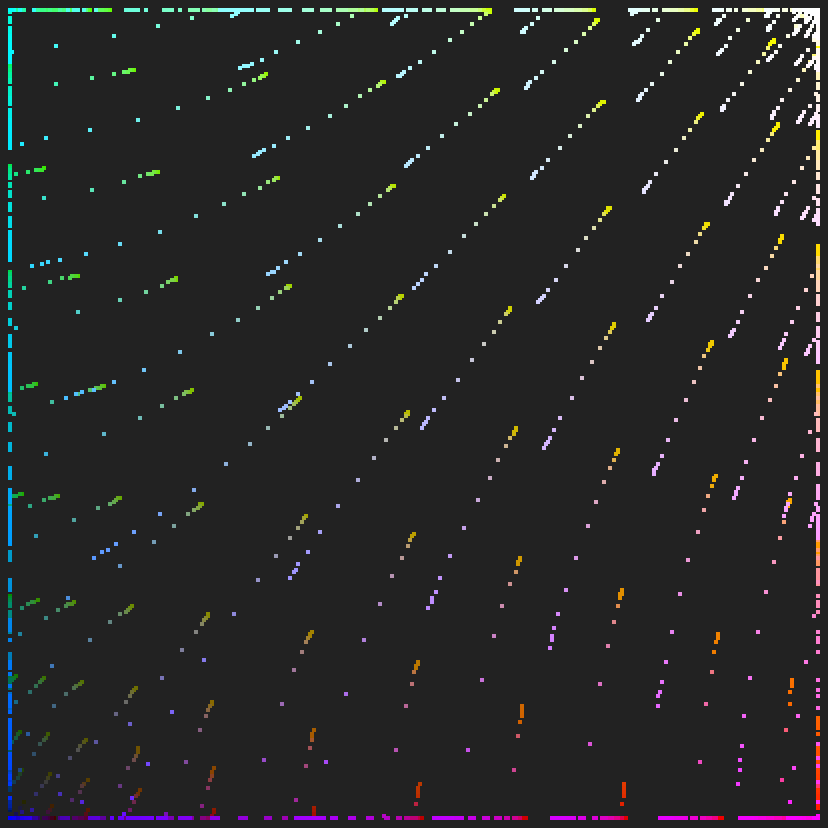 |  |
| right |  |  | 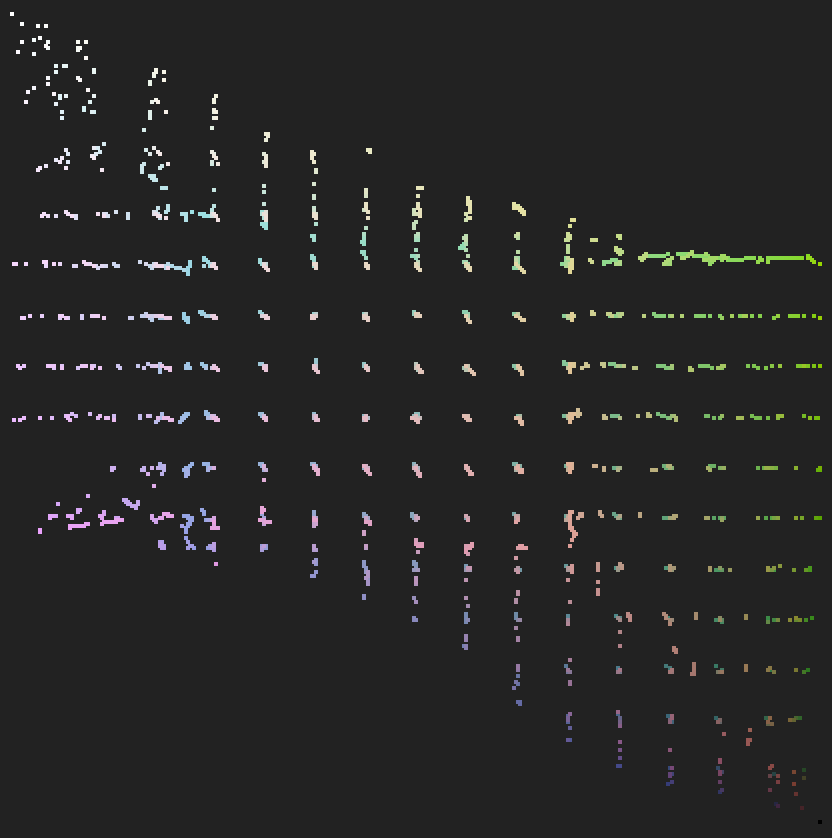 |
| perspective |  | 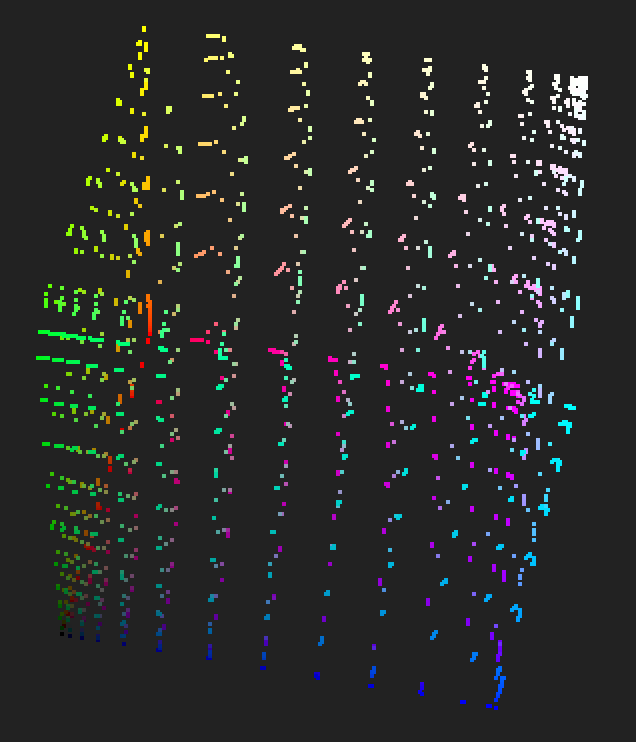 | 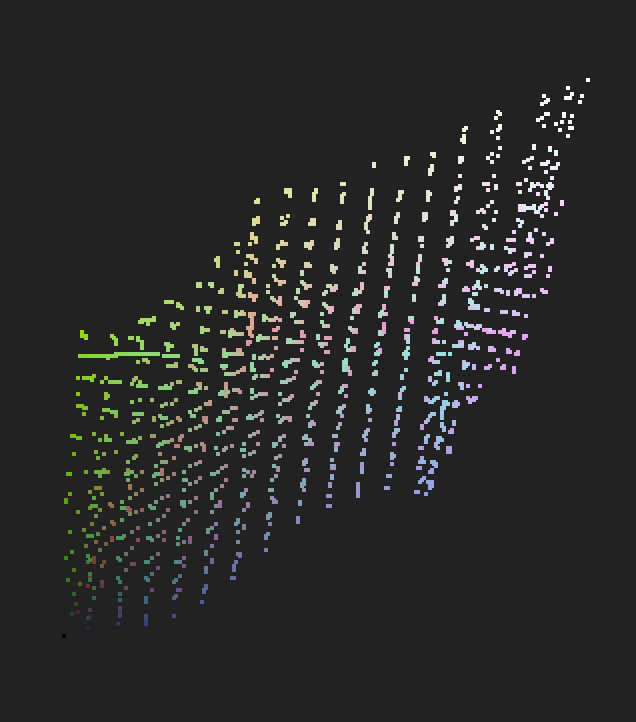 |
最后,可以从实际拍摄的素材中来查看人眼实际感觉上的差异,可以认为非常小
| 原始Slog SGamut3.cine | 转换为s709 |
|---|---|
 |  |
| s709+反向LUT | 差异(放大64倍) |
 |  |
| 差异统计信息 | |
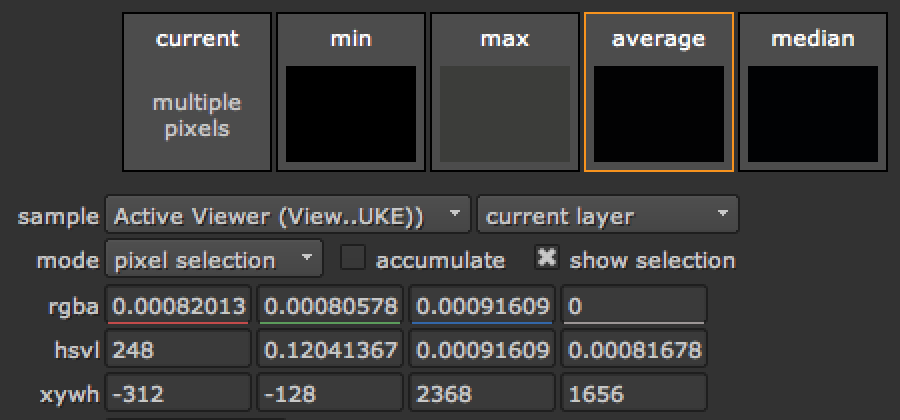 |
潜在的问题
目前的算法,没有对求解得到的反向结果进行平滑。这就导致了反向LUT 其实存在轻微的抖动(jitter)。
个人理解,这种抖动主要是由于在进行梯度下降的过程中,优化结果在真实解的附近来回跳动,而临近的每一个lattice 都会出现不同的跳动。
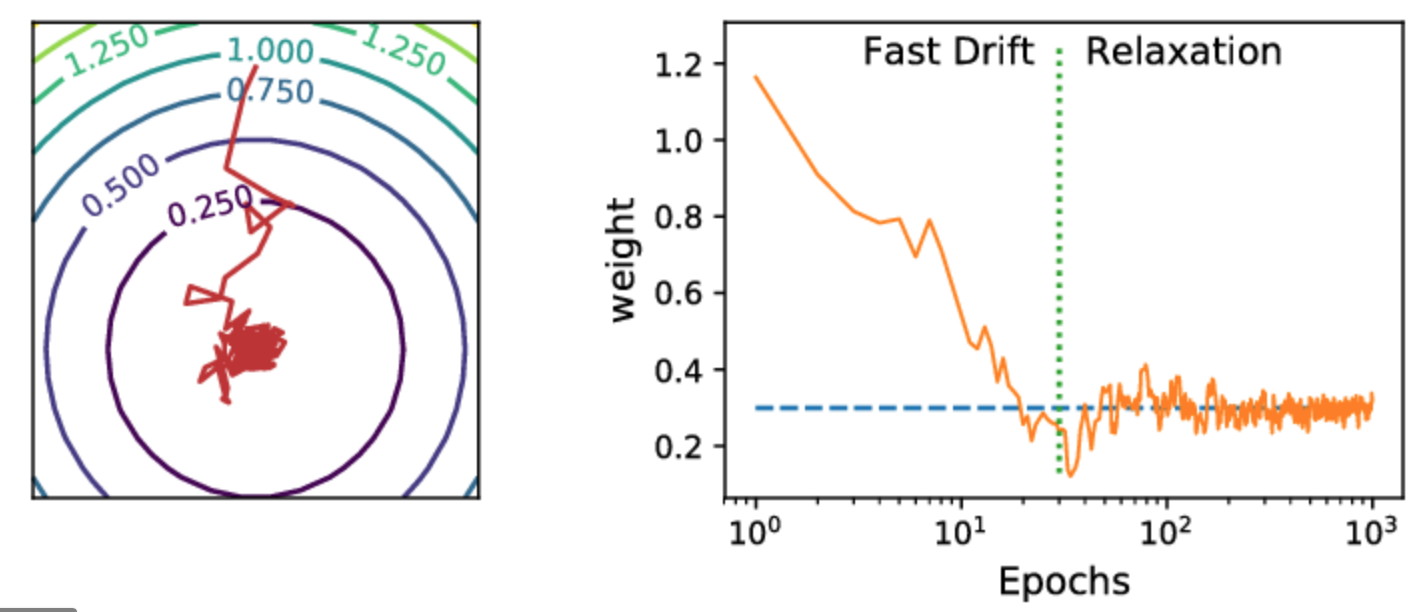
在图像上直观的反应,就是平滑色彩的过度不是非常平滑。
| 原始图像(gain = 4) | 正向+反向LUT 抵消(gian=4) |
|---|---|
 |  |
之后,可以考虑对所有的反向求解point,进行laplacian smooth
应该可以优化这个问题。(暂时没有进行测试)
我可以认为如果LUT 中相邻lattice 的色彩数值应该是平滑的,如果出现了抖动,那就可能造成这个问题:
| R | G | B |
|---|---|---|
 |  |  |
参考阅读
https://colour.readthedocs.io/en/develop/_modules/colour/algebra/interpolation.html
(Colour 库 实现的 tetrahedral 3D LUT 插值算法,经过验证和nuke 中的结果完全一致)
相关文件下载
文中的代码和对应 sony invert lut 文件
文件下载
点击购买,或者扫描二维码


